Simple vs Compound Return: What’s the Difference?
Learn how simple and compound returns work, their key differences, and which one matters most for your investing or borrowing decisions.
Pro Stock Tracker
Ever heard the phrase, “Let your money work for you”? Well, how it works and how hard it works depends heavily on whether your returns are simple or compounded.
While both are ways to measure how much your money grows over time, they work very differently. One is like a slow, steady jog. The other is more like a snowball rolling downhill, gathering more and more speed as it goes.
In this article, we’ll break down the difference between simple return and compound return, when each is used, and why understanding the two can help you make smarter investment and borrowing decisions.
What is a simple return?
A simple return is a fixed and predictable way to calculate how much your investment earns over time. It applies a constant rate of return to your original investment (called the principal) and doesn’t consider any reinvested earnings. In other words, your gains are always based on the initial amount, nothing more.
Here’s the formula:
Simple return = P × i × n
Where:
- P = principal (your initial investment)
- i = interest rate per period (as a decimal)
- n = number of periods
Let’s walk through an example.
If you invest $1,000 at a 5% annual return for 3 years, your total simple return would be:
$1,000 × 0.05 × 3 = $150
That means your investment earns $50 per year, for a total of $150 in interest. Each year’s gain is the same, and the interest doesn’t build on itself.
This makes simple return easy to understand and calculate. It’s often used for short-term investments, personal loans, or fixed-rate financial products like certain bonds.
However, since it doesn’t reinvest your gains, it doesn’t reflect how your money could grow over the long term, and that’s where compound return comes in.
What is a compound return?
Compound return, also known as compounded growth or interest, is where the magic happens.
Instead of calculating return only on your original investment, compound return calculates growth on your original money plus any previous gains. In other words, you earn interest on your interest.
Think of it like this: if you plant a tree and it grows fruit, and then you plant the seeds from that fruit, you’ll have more trees growing even more fruit. That’s compounding.
Here’s the compound return formula:
A = P × (1 + r/n)^(n × t)
Where:
- A = final amount
- P = principal (initial investment)
- r = interest rate per period (as a decimal)
- n = number of compounding intervals per period
- t = number of periods
Let’s apply that with an example.
Say you invest $1,000 at 5% annual interest, compounded yearly, for 3 years:
A = 1,000 × (1 + 0.05/1)^(1×3) = $1,157.63
You’d earn $157.63, not just $150 like you would with simple interest. Why? Because you’re also earning interest on the $50 gain from year one, and the additional gain from year two. That’s compounding at work.
Simple vs compound return: side-by-side example
Let’s see how they compare over time.
| Year | Simple return (5%) | Compound return (5%) |
|---|---|---|
| 1 | $1,050 | $1,050 |
| 2 | $1,100 | $1,102.50 |
| 3 | $1,150 | $1,157.63 |
| 5 | $1,250 | $1,276.28 |
| 10 | $1,500 | $1,628.89 |
With compound return, the longer you let your investment grow, the bigger the gap becomes.
Growth pattern: linear vs exponential
The key difference between simple and compound return lies in how they grow:
- Simple return grows in a straight line.
Each period earns the same amount without any surprises. - Compound return grows exponentially.
The gains start small, but over time, they accelerate. It’s like rolling a snowball downhill; the longer it rolls, the bigger it gets.
So if you’re investing for the short term, the difference might not be huge. But over 10, 20, or 30 years? The compound effect can be dramatic.
Here’s how it looks in practice:
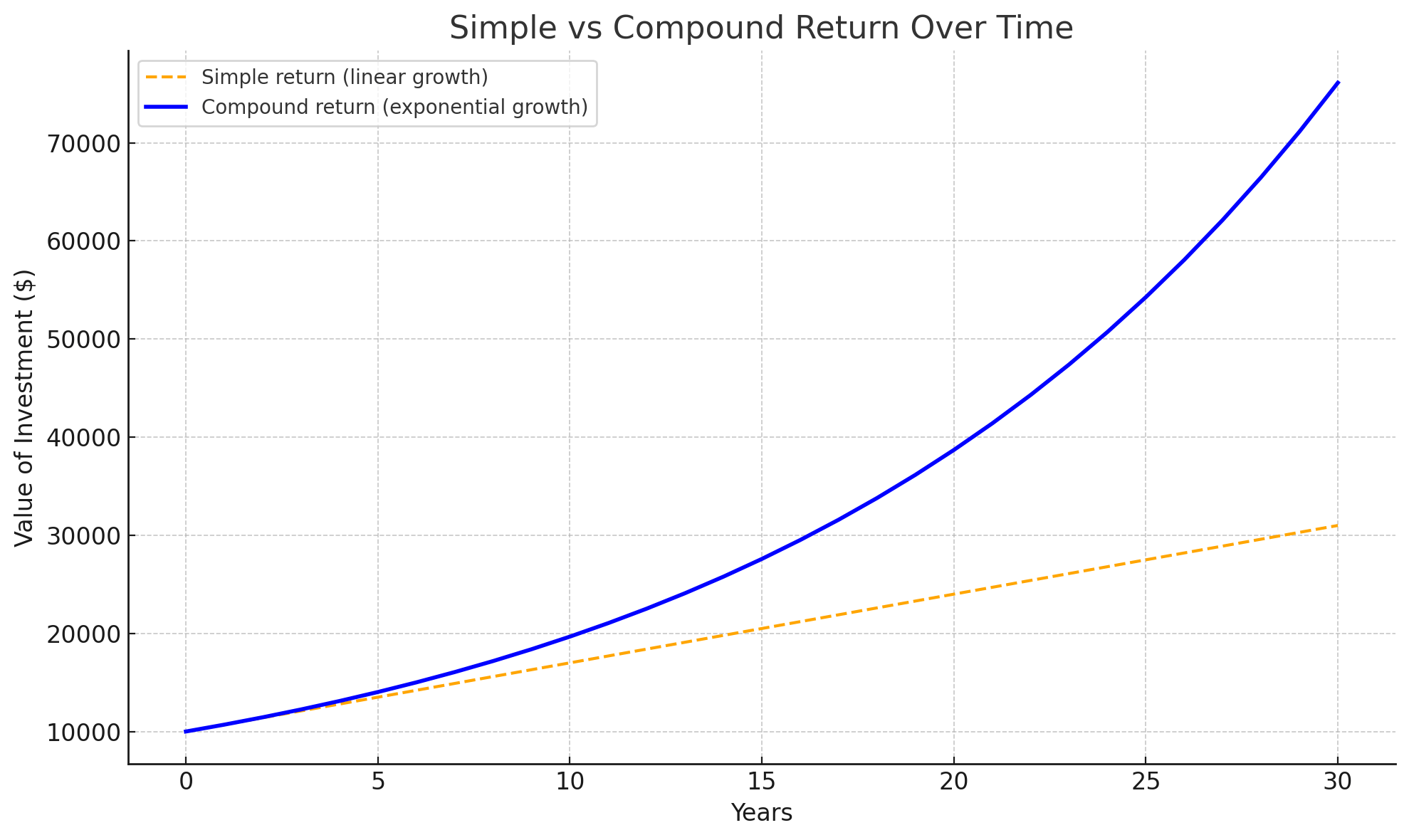
As the chart shows, both returns start at the same place, but while simple return increases steadily, compound return begins to pull ahead and eventually leaves it far behind. That’s the true power of reinvesting your gains over time.
When is simple return used?
Simple return is commonly used in:
- Short-term investments
- Basic loan calculations
- Certain fixed-income instruments (like short-duration bonds)
- Performance snapshots (e.g., “This stock returned 8% last year”)
It’s easy to calculate and understand, which makes it useful for quick comparisons or straightforward loans where interest doesn’t roll over.
When is compound return used?
Compound return is the standard for:
- Long-term investments (stocks, ETFs, mutual funds)
- Savings accounts
- Reinvestment scenarios
- Loan amortization schedules
- Comparing fund or portfolio performance over time
Any time your returns are reinvested, whether it's dividends, interest, or gains, you’re dealing with compounding.
Why compound return is the investor’s best friend
If you’ve ever heard Warren Buffett talk about getting rich slowly, it’s because of compound returns.
Here’s a simple example to show just how powerful compounding can be.
Let’s say:
- You invest $5,000 per year
- The average annual return is 7%
- You invest for 30 years
To calculate the compound return with regular yearly contributions, we use the Future Value of an Ordinary Annuity formula:
FV = P × [((1 + r)^n – 1) ÷ r]
Where:
- P = yearly contribution ($5,000)
- r = interest rate per period (0.07)
- n = number of periods (30 years)
Plug that in and you get:
FV = 5,000 × [((1 + 0.07)^30 – 1) ÷ 0.07] = $472,304
Now let’s compare that to a scenario with no compounding, just applying simple interest on each yearly contribution.
Each $5,000 contribution earns interest for a different number of years: the first earns for 30 years, the second for 29, the third for 28, and so on, all the way to the final year’s contribution, which earns nothing.
So we calculate the total simple interest like this:
Interest = $5,000 × 0.07 × (30 + 29 + 28 + … + 1 )
The sum of those years is 465, so:
Interest = $5,000 × 0.07 × 465 = $162,750
Principal = $5,000 × 30 = $150,000
Total = $312,750
That’s a decent return, but it’s still nearly $160,000 less than what compounding delivers. All you did was reinvest the gains, and over time, that one change added up to a six-figure difference.
The takeaway? Time + compounding = wealth.
The rule of 72: a compounding shortcut
Want to know how long it’ll take for your investment to double? Use the Rule of 72.
Just divide 72 by your annual return rate, and that’s approximately how many years it’ll take to double your money.
For example:
- At 6%, it takes about 12 years (72/6) to double.
- At 9%, it takes about 8 years (72/9).
It’s not exact, but it’s pretty close and incredibly useful when planning long-term goals.
Important: The Rule of 72 assumes annual compounding. It doesn’t apply accurately if interest is compounded monthly, quarterly, or daily.
How compounding frequency affects growth
Compounding doesn’t always happen annually. It can also happen:
- Semi-annually
- Quarterly
- Monthly
- Daily
The more frequently your returns are compounded, the faster your money grows. That’s because interest is calculated and added to your balance more often, giving your money more chances to earn interest on itself.
To see this in action, let’s look at an example below:
You invest $10,000 at a 5% interest rate for 3 years.
We’ll use the standard compound interest formula:
A = P × (1 + r / n)^(n × t)
Where:
- P = $10,000 (initial investment)
- r = 0.05 (5% annual interest)
- t = 3 years
- n = number of compounding periods per year (varies with frequency)
Here’s how the final amount changes depending on how often interest is compounded:
| Frequency | Final amount |
|---|---|
| Annually (n = 1) | $11,576.25 |
| Quarterly (n = 4) | $11,607.55 |
| Monthly (n = 12) | $11,614.72 |
| Daily (n = 365) | $11,618.22 |
As you can see, the more often interest is added, the more your investment grows, even if it's just by a few extra dollars in the short term. The reason is that each time interest is applied, it slightly increases your balance, which then earns even more interest in the next round.
The difference might seem small over just 3 years, but stretch that to 30 years and the gap becomes much more significant. That’s the power of compounding frequency in action.
Where simple return can actually be better
Not everything about compound interest is sunshine and roses.
If you’re borrowing money, compound interest can work against you.
Think of credit cards. If you carry a balance, the interest is compounded daily. That means you're paying interest on interest on interest, and that adds up fast.
In contrast, loans with simple interest, like many personal or auto loans, are easier to manage. You pay the same interest each month, and it doesn’t snowball.
So, when you’re borrowing, simple interest = better.
When you’re investing, compound return = better.
What about compound annual growth rate (CAGR)?
CAGR is a special kind of compound return that smooths out the ups and downs.
Let’s say your portfolio:
- Grew 20% in year 1
- Lost 10% in year 2
- Gained 15% in year 3
That’s a rollercoaster, right?
CAGR calculates the average annual growth rate over those 3 years, as if it had grown at a steady rate the whole time.
It’s useful for:
- Comparing fund performance
- Evaluating investment strategies
- Measuring portfolio growth over time
If you’re serious about tracking your portfolio performance, CAGR gives a clearer long-term picture than just looking at year-by-year returns.
Let’s recap: key differences at a glance
| Feature | Simple return | Compound return |
|---|---|---|
| Growth style | Linear | Exponential |
| Calculated on | Initial investment only | Investment + prior returns |
| Best for | Short-term, loans | Long-term investing |
| Reinvestment effect | None | Yes, returns are reinvested |
| Formula | A = P × (1 + i × n) | A = P × (1 + r/n)n × t |
| Advantage for investor | Predictable, easy to follow | Bigger gains over long term |
| Risk when borrowing | Lower | Can become very costly |
Which one should you focus on?
Here’s the golden rule:
- If you’re borrowing → Look for simple interest loans
- If you’re investing → Let compound interest do its thing
The key is knowing what you’re working with and how it impacts your money over time.
Understanding this difference can save you thousands in interest payments or help you build a bigger nest egg faster.
Conclusion: let compounding work for you, not against you
Simple return might be easier to understand, but compound return is what really drives wealth in the long run.
Whether you're saving for retirement, investing in the markets, or paying off debt, knowing the difference between the two gives you the upper hand. It helps you make smarter choices, avoid nasty surprises, and plan with clarity.
So start early, stay consistent, and remember: when it comes to building wealth, compound return is your most loyal ally.
This article is part of Pro Stock Tracker's Performance Methodology Series, exploring different approaches to measuring investment returns and why we've developed superior alternatives.
Disclaimer: The information provided in this article is for general informational purposes only and does not constitute specific advice, including but not limited to financial, investment, or legal advice. While we strive to ensure the accuracy and completeness of the information, we make no guarantees and assume no liability for any actions taken based on the content provided. Please consult with a qualified professional for advice tailored to your individual circumstances.

